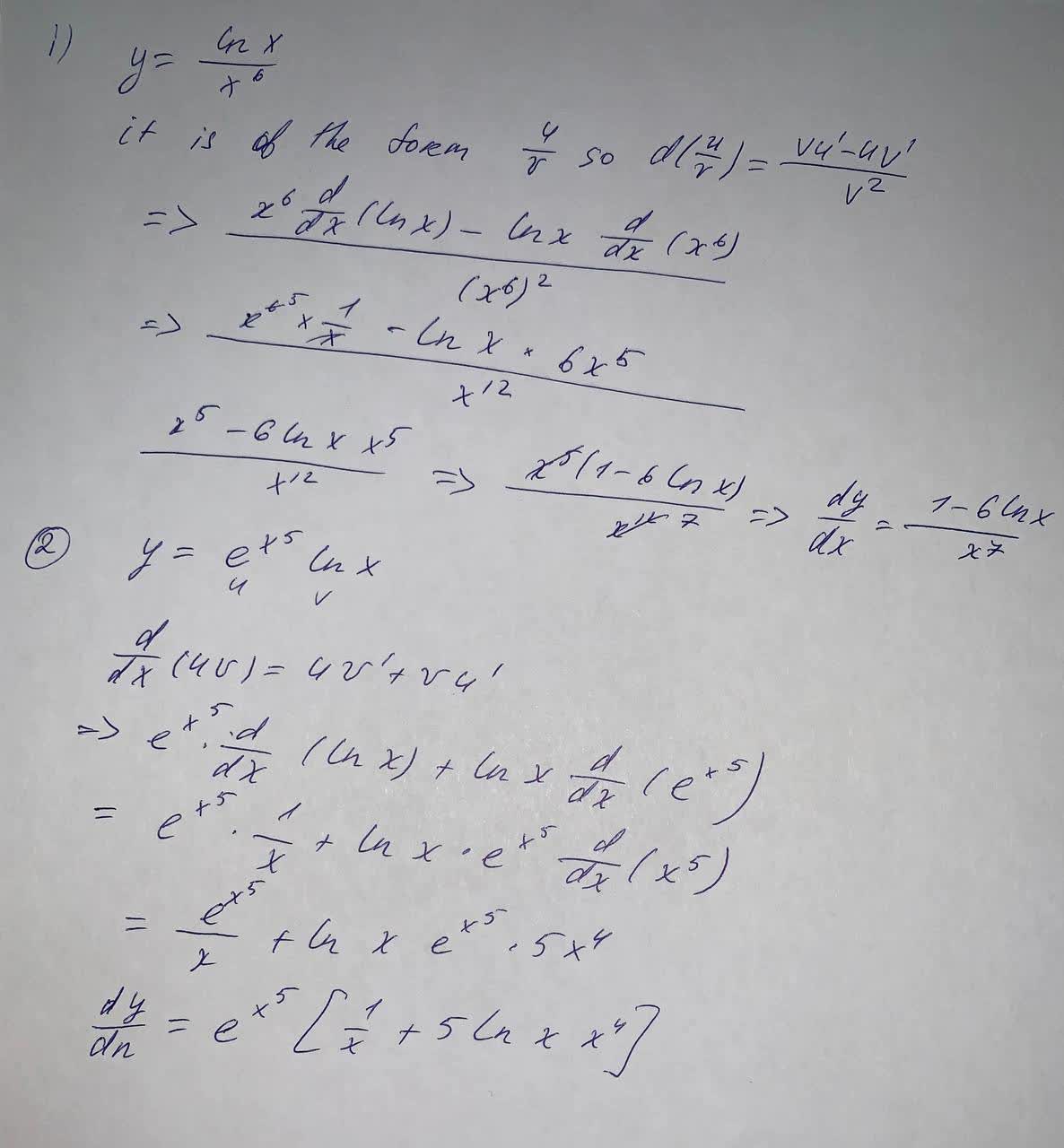
Find The Derivative Y Frac Ln X X 6 Y E X 5 Ln X Find The Indicated Derivative Of Plainmath
Solution To find the xderivative, we consider y to be constant and apply the onevariable Chain Rule formula d dx (f10) = 10f9 df dx from Section 28 We obtain ∂ ∂x (x2y3 sinx)10 = 10(x2y3 sinx)9 ∂ ∂x (x2y3 sinx) = 10(x2y3 sinx)9(2xy3 cosx) Similarly, we find the yderivative by treating x as a constant and using the samePartially differentiate functions stepbystep \square!
Derivative of ln(x^2 y^2) with respect to y
Derivative of ln(x^2 y^2) with respect to y-If y = ln x then e y = x Now implicitly take the derivative of both sides with respect to x remembering to multiply by dy/dx on the left hand side since it is given in terms of y not x e y dy/dx = 1 From the inverse definition, we can substitute xSin y = x We next take the derivative of both sides of the equation and solve for y = dy dx sin y = x (cos y) y = 1 1 y = cos y We want to rewrite this in terms of x = sin y Luckily there is a simple trig identity relating cos y to sin y We can solve it for cos y and "plug in" cos 2

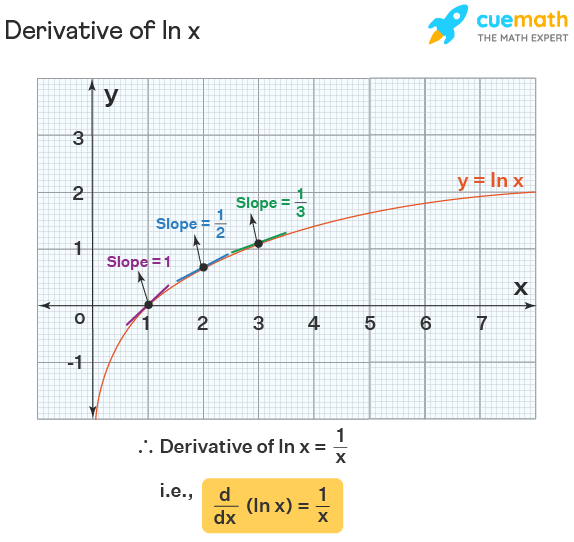
Solving The Derivative Of Ln X Video Lesson Transcript Study Com
How to differentiate the natural exponential function using chain rule d/dx of e^(x^2)We treat y as a constant, so y 3 is also a constant (imagine y=7, then 7 3 =343 is also a constant), and the derivative of a constant is 0D dx (x 2) d dx (y 2) = d dx (r 2) Let's solve each term Use the Power Rule d dx (x2) = 2x Use the Chain Rule (explained below) d dx (y2) = 2y dy dx r 2 is a constant, so its derivative is 0 d dx (r2) = 0 Which gives us 2x 2y dy dx = 0 Collect all the dy dx on one side y dy dx = −x
In this case we call h′(b) h ′ ( b) the partial derivative of f (x,y) f ( x, y) with respect to y y at (a,b) ( a, b) and we denote it as follows, f y(a,b) = 6a2b2 f y ( a, b) = 6 a 2 b 2 Note that these two partial derivatives are sometimes called the first order partial derivatives Just as with functions of one variable we can have Find the derivative of h with respect to u if h \u03c02u a \u03c02u b 2u ln \u03c0 c 2\u03c02u ln \u03c0 So I feel we would get$$\frac{\partial}{\partial x} \ln(x^2y^2)=\frac{2x}{x^2y^2}$$ and with respect to $y$ $$\frac{\partial}{\partial y} \ln(x^2y^2)=\frac{2y}{x^2y^2}$$ Is that right?
Derivative of ln(x^2 y^2) with respect to yのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
2 | 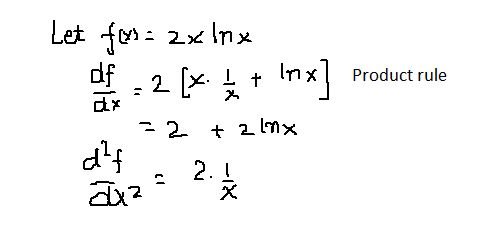 2 | 2 |
 2 | 2 |  2 |
 2 |  2 | 2 |
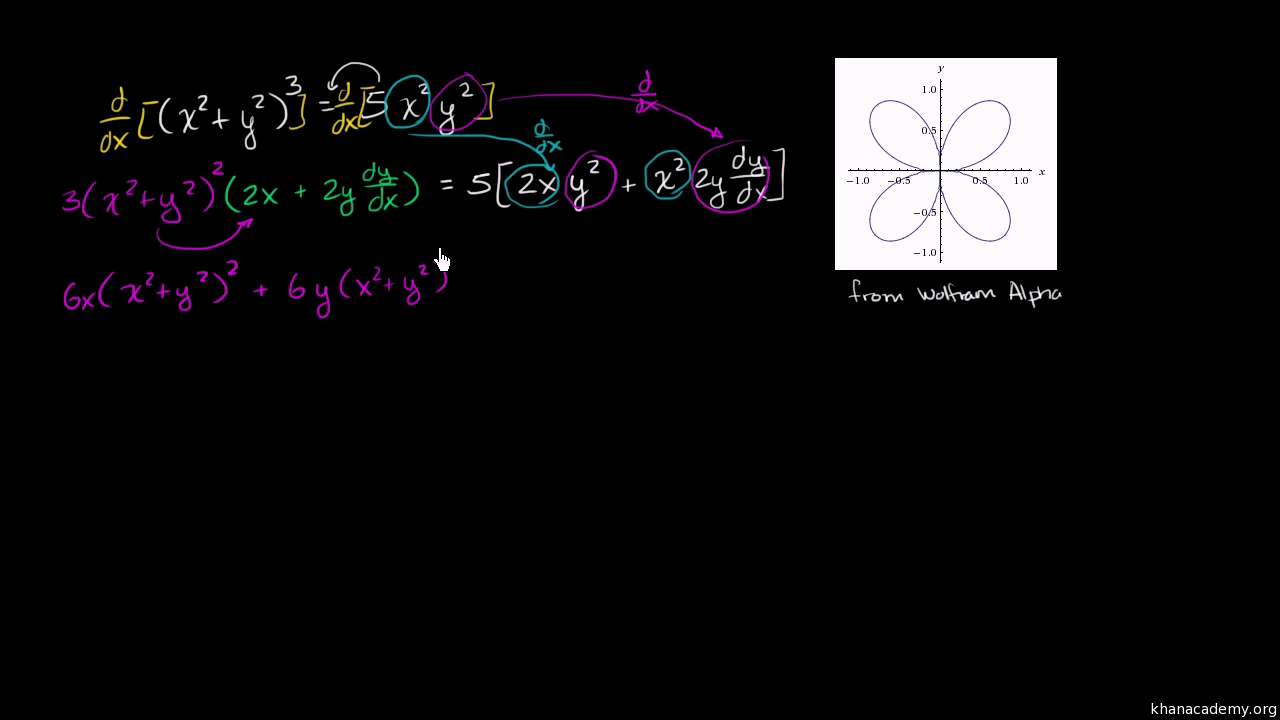 2 |  2 | 2 |
2 |  2 |  2 |
 2 | 2 |  2 |
 2 | 2 |  2 |
 2 | 2 | 2 |
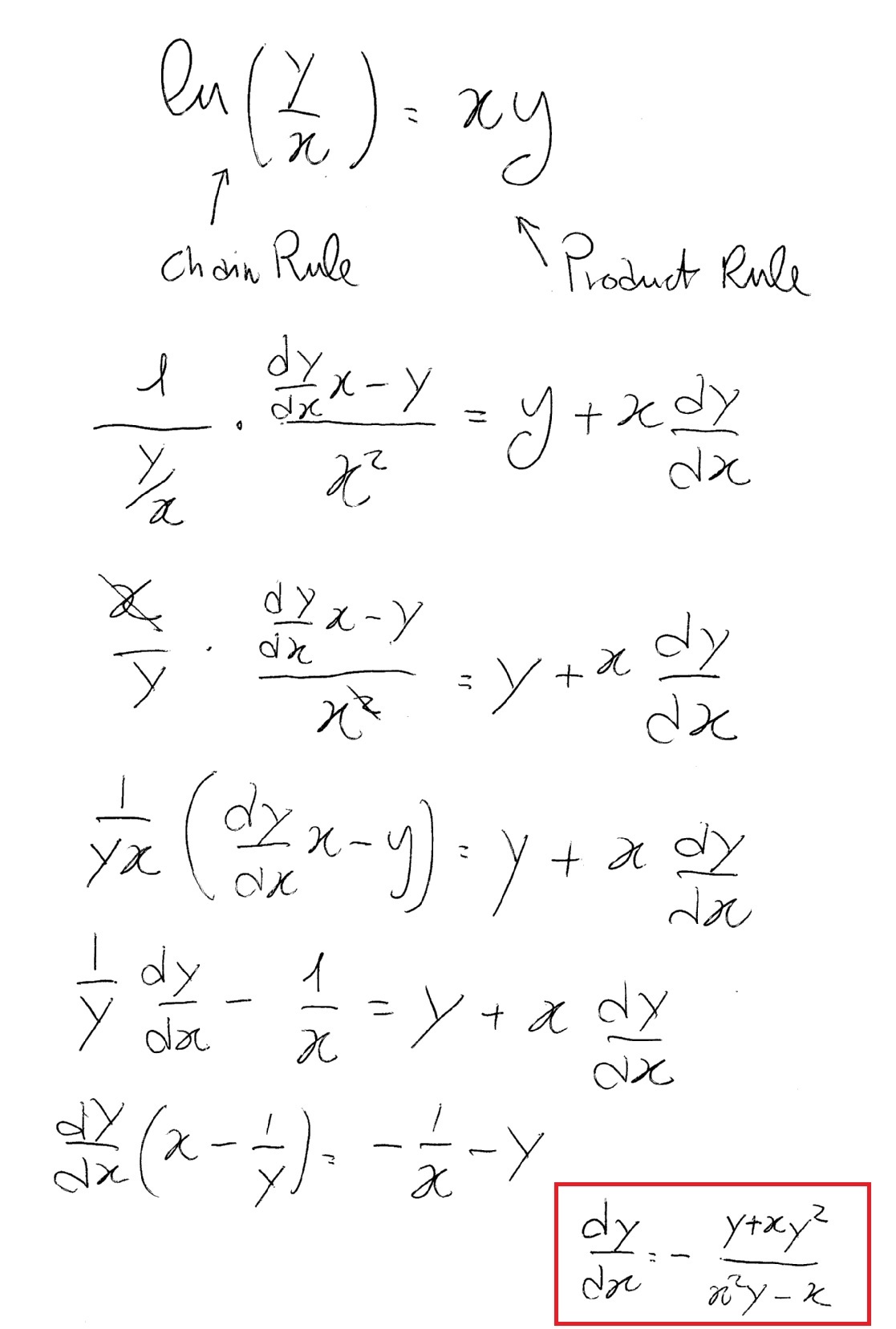 2 | 2 | 2 |
 2 |  2 |  2 |
2 |  2 |  2 |
 2 | 2 |  2 |
2 |  2 |  2 |
 2 | 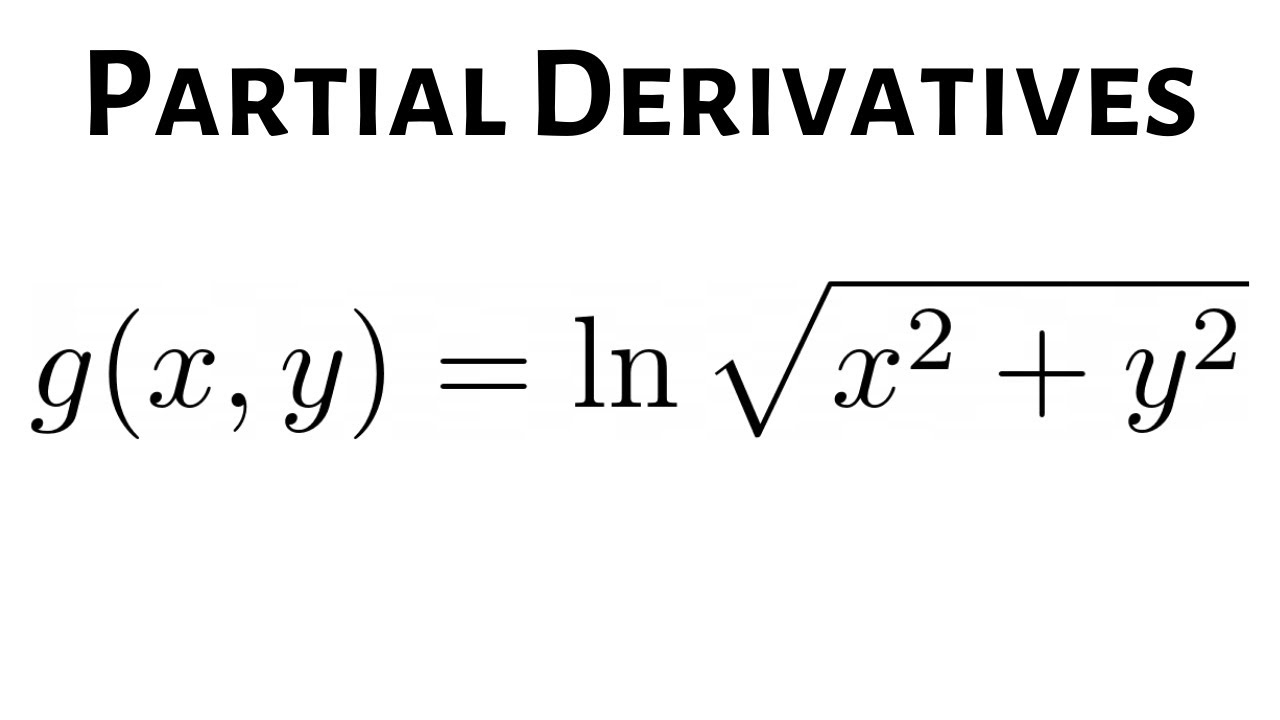 2 |  2 |
2 |  2 | 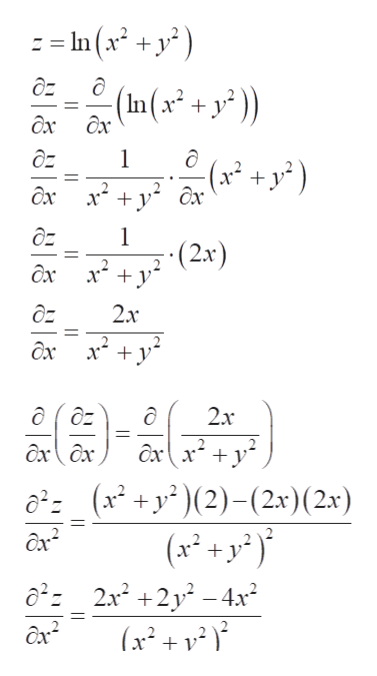 2 |
 2 | 2 | 2 |
 2 | 2 | 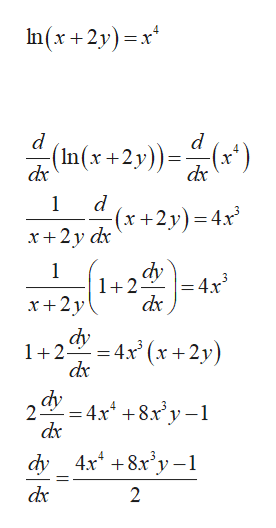 2 |
 2 |  2 |  2 |
 2 |  2 |  2 |
 2 |  2 | 2 |
 2 |  2 | 2 |
 2 | 2 |  2 |
2 | 2 | 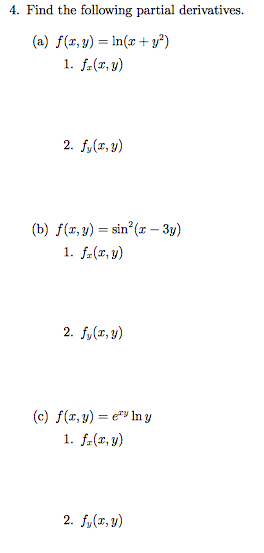 2 |
2 |  2 | 2 |
 2 |  2 |  2 |
 2 |  2 |  2 |
2 |  2 |  2 |
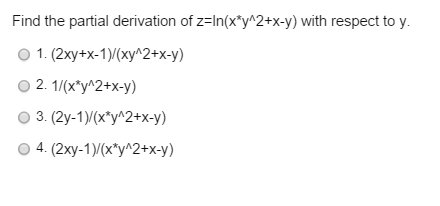 2 | 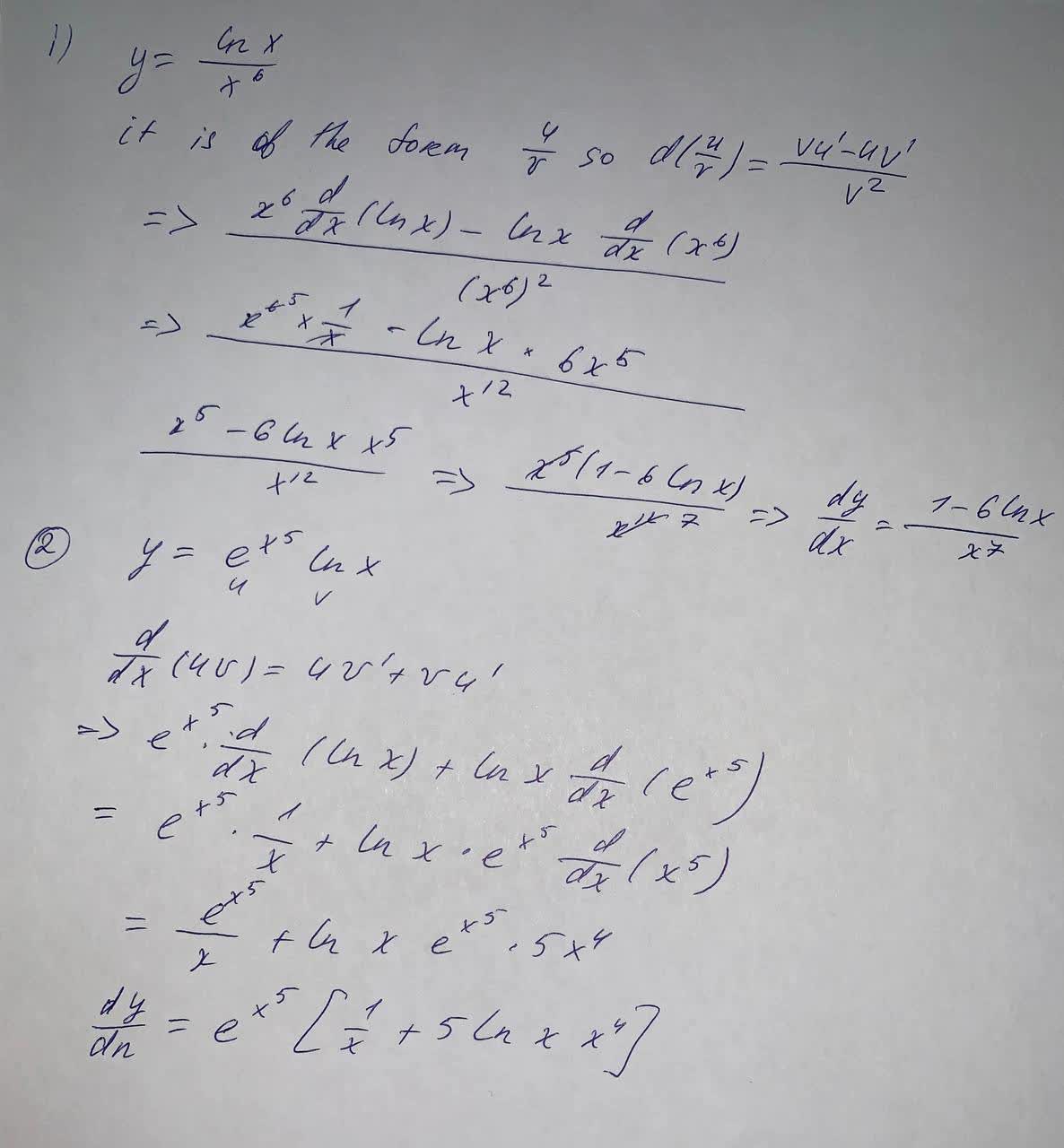 2 |  2 |
 2 |  2 |  2 |
 2 | 2 |  2 |
 2 |  2 | 2 |
2 |  2 |  2 |
 2 | 2 | 2 |
 2 |  2 |  2 |
 2 |  2 |
Expert Answer Who are the experts?= 3x4y2 8x2 4y3 (Note x fixed, y independent variable, z dependent variable) 2 If z = f(x,y) = (x2 y3)10 ln(x), then the partial derivatives are ∂z ∂x = x(x2 y3)9 1 x (Note We used the chain rule on the first term) ∂z ∂y = 30y 2(x y3)9 (Note Chain rule again, and second term has no y) 3 If z = f(x,y) = xexy, then the partial derivatives are ∂z





0 件のコメント:
コメントを投稿